在学习数学的过程中，会接触到数学世界中有趣的名词，比如说：辛空间、酉空间、奇点、极点、正态、正交、正规、同伦、同胚、同调……

每个学科可能都有学术名词翻译的问题，我国的翻译学家在翻译的时候遵从着信达雅的原则，在数学学科中，有许多像正合、流形、共轭、拓扑等等自然贴切的名词，但也出现了像辛空间、酉空间这样高深的术语，今天就让我们来聊聊数学中一些或让人啧啧称奇或让人想要刨根究底的名词翻译吧：

1

共轭（conjugate）

共轭这个名词并非数学专有，在化学中也有共轭化学键。

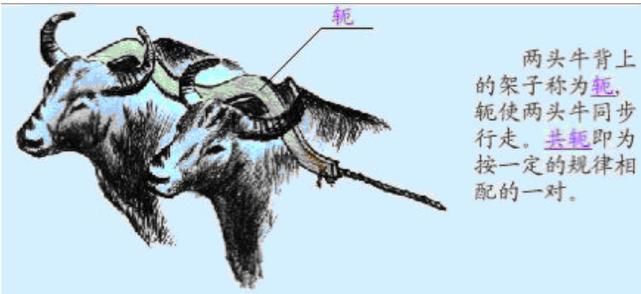
这是一个简单自然的直译，conjugate=common?jugum，jugum即轭：指连结两个结构的凹或嵴的通名。

如此，复数的共轭就很好理解，a+bi与a-bi中a和bi就是连接+与-两个结构的轭。十分形象。

2

流形（manifold）

manifold=many?fold，可以理解为许多的小曲面片，在不知道流形的定义的情况下看这个中文翻译和英文，不能说是截然不同，只能说是毫不相干……

然而，在了解流形的定义和性质之后，就会觉得manifold和流形两个名词各有千秋：流形的局部可以对应到一个欧式空间，所以可以称为Manifold——许多个对应于欧式空间的小局部黏结而成的一个几何形体；而流形这个翻译，有几何形体在流动的意思，把握住了微分几何中流形不应该被看做一个僵硬的由固定的点构成的集合、本身具有“柔性”的这一特点。

从这个例子来看，数学家在专有名词进行翻译的时候，不仅仅会考虑直译的“信”，还会考虑它本身的定义及具有的性质，进一步和本土的习惯结合起来，在达成更高级的“信”的同时也达成了“达”和“雅”；

类似的还有毕达哥拉斯定理翻译为勾股定理，不是简单的直译，而是很好地结合了本土文化以及人的习惯，相比毕达哥拉斯的繁琐与不知所然，勾三股四弦五让我们一下子领会到了这个定理的精神，简单明了，朗朗上口。

3

拓扑（topology）

拓扑这个翻译妙就妙在在不知道英文名词的情况下完全不会想到这个词是音译的，而且即使对高等数学没有了解，也会不自觉地把拓扑和图形联系起来，料想拓扑应该与图形、几何等等相关……

topology的直译是地质学，最早指研究地形、地貌相类似的有关学科。几何拓扑学是十九世纪形成的一门数学分支，它属于几何学的范畴，是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的一个学科。它只考虑物体间的位置关系而不考虑它们的形状和大小。

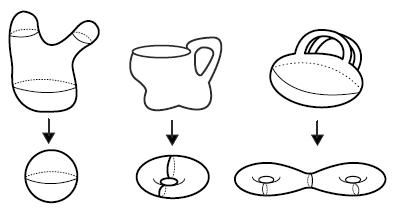显然，相对于地质学这个直译，拓扑显得“数学”多了，而且音意俱达，贴合自然。

4

运筹学（operations?research）

中文对运筹学的翻译常常被誉为是“信、达、雅”的典范，现代运筹学的基本内容就是运用统计学、数学模型、算法等方法去寻找复杂问题的最优解或者近似最优解。

运筹一词出于《史记》中刘邦赞张良的名句“夫运筹帷幄之中，决胜千里之外，吾不如子房。”，在有文化底蕴的同时又很好地传达出了运筹学的内涵。

5

辛空间、酉空间

在第一次看到辛空间和酉空间这两个名词的时候，小编很认真地扒着手指头数了数辛和酉分别在天干地支的第几位，并开始好奇维数为8的空间和维数为10的空间是否有什么特殊性质，怀疑这与正十七边形有异曲同工之妙……

等到小编看完定义，才发现不是一回事，事实证明，面对一个崭新的定义千万不要主观臆断以及先入为主，不然……不然你可能会像小编一样，很难把对辛空间和酉空间的初印象从脑海中抹去。

symplectic linear space中的sympletic是一个造词，为微分几何中的概念，并不容易翻译，现一般翻译为耦对的，相比音译有传统文化加持的辛空间，耦对线性空间较为符合辛空间的定义。

unitery??space 字面意义是单位空间，强调了酉空间必有标准正交基的性质，而酉空间这个音译并不能凸显这类复线性空间的任何性质。

这两个翻译经常被认为是不好的翻译，字面上晦涩，也无法传达出定义的内涵。

6

动力系统（dynamical?system）

没想到吧，动力系统是我数学的概念。诚然，第一次听说动力系统这个概念的时候容易将其误解为工科或者物理等专业的概念。大体来说，动力系统描述了一个随着时间演变的体系。虽然听起来有些别扭，但还是能表达出一定的内涵的。

文章来源：《应用数学》 网址: http://www.yysxzzs.cn/zonghexinwen/2021/0522/647.html